En este post nos valemos de matemáticas elementales y un nuevo planteamiento para estudiar las propiedades de la energía del vacío como un simple fractal. Descubrimos las posibles dimensiones compactadas de la teoría de cuerdas y su importancia en la propia naturaleza del cuanto de acción (en muchas entradas de este blog, podeís leerlo en español, y en la referencia final de la Universidad de Puebla, México, o en Mi_ciencia_abierta).
Abstract
In this letter, we use
elementary mathematics and a novel approach to study the properties of vacuum
energy as a simple fractal. By applying fractal geometry, we can identify the
compact dimensions and gain a better understanding of their significance in the
fundamental nature of quantum action.
Keywords: Vacuum energy, compacted dimensions, relative
fractal dimension, transition of dimensions, hypothetical quantum generalization
1
Introduction
The existence of Planck's
quantum of action transforms Newton's classical and deterministic universe into
a quantum universe, governed by Heisenberg's uncertainty principle. The vacuum
contains a zero-point energy (ZPE) with a higher value as the distance
considered becomes smaller. The minimum length, known as Planck's length (lp),
is associated with a maximum energy called Planck's energy (Ep). For a distance
n(lp), the associated energy is (Ep)/n, where "n" is a natural
number. This property, conserved across all known scales, will assist us in
analyzing this fractal. We will see that the relationship between ordinary
dimensions and compact dimensions may have played an essential role in Planck’s
quantum of action.
2 Fractal
dimension, study of Brownian motion and the Koch snowflake
Fractal dimension is
composed of two components: the topological dimension and a dimensional
coefficient (topol_dim + dimens_coef). The more irregular the fractal, the
higher the dimensional coefficient. For the purposes of our
study, it is particularly interesting to examine simple fractals that possess a
topological dimension of 1, such as the fractal path of Brownian motion.
Brownian motion (also
known as Brownian movement) refers to various physical phenomena characterized
by small, random fluctuations in some quantity. It was named after the Scottish
botanist Robert Brown, who first studied these fluctuations in 1827
(britannica.com, December 23, 2021).
Top
of Form
To move N effective
steps in a straight line along one dimension, a particle moving with Brownian
motion must take N2 total steps across two or more dimensions. The
fractal dimension, a basic property of fractal lines [1], can be calculated
using the relation log(N2) / log(N) = 2. In this case, the
topological dimension is 1 and the dimensional coefficient is also 1. The value
of 2 for the fractal dimension indicates that a linear movement, of topological
dimension 1, can fill a plane of topological dimension 2.
In Brownian motion, and in
general, fractal value = N2 = distancefractal_dimension.
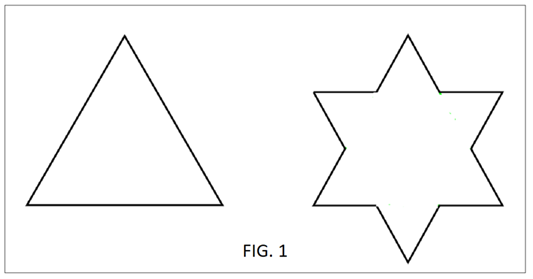
This can also be observed in
the Koch curve, as shown in Figure 1. In the first iteration, the side that
measures 3 segments becomes 4 segments. The fractal dimension is calculated as
log 4 / log 3 = 1.26186. In one dimension, 3 segments become 4 segments in two
dimensions (the plane):4= 31,26186, 4=3fractal_dimension
(Mandelbrot, 1987).
3 Fractal
dimension of vacuum energy
We know the dependence
of vacuum energy on distance:
En = Ep
/ n = (Ep) (distance)-1.
If we live in hyperspace
(according to string theory), we know the dependence of vacuum energy on
distance in that space. Let En(hyper) be the value of the energy in
hyperspace. Then:
log (En(hyper))
/ log (En) = -1
This implies that vacuum
energy is proportional to distance in hyperspace. Although energy has no
topological dimension of 1, the quotient of the two logarithms behaves
similarly to the case of Brownian motion. When comparing two energies, the
topological dimension no longer matters because the result is a relative
fractal dimension:
Relative fractal dimension =
(topol_dim. + dimens_coef.)/(topol_dim.). To simplify we will write:
Relat_fr_dim. = (δ+ε)/δ (1).
So, we have: Relat_fr_dim=
Log (En(hyper)) / log (En)= -1 = (δ+ε)/δ.
The -1 value reminds us of
the compacted dimensions of the string theory, since while a positive
dimensional coefficient indicates that the fractal occupies a space greater
than its topological dimension, a negative dimensional coefficient indicates
dimension compaction (Ruiz-Fargueta,
2004). The situation indicates a transition of dimensions such that:
T: δ àδ−ε.
The expression (1), with this
transition becomes: δ/(δ−ε) (2).
If the dimensional
coefficient is the same as the number of compact dimensions.
Expression (2) is consistent
with the value -1, since for d = 3 it gives us the value -6 for the number of
compact dimensions, which coincides with the value predicted by string theory.
Applying these values to the expression (1):
(δ+ε) / δ = (3+6)/3= 3 .
3 is the relative fractal dimension of the
vacuum energy, 9 its true fractal dimension.
The same result is found in
the following equivalent transformations:
T11: 1/n→ n } log(n)/log(1/n) = -1. Apparent
result in relative fractal dimension.
T12: n→ n3 } log(n3)/log(n) = 3. True
result in relative fractal dimension.
The T11 transformation gives us the apparent result -1. But
the transformation T12 gives us the true result 3.
.
4
Generalization and possible transition of dimensions
The value -1 is the result of
En, as a function of distance, in the expression
(En)(n) <Constant, where
we have replaced the time (energy-time uncertainty principle) by the space (n)
traveled by the light in that time. If in this expression we add a fictitious
coefficient f, we will have:
(En) (nf)
<Constant (3) (Hypothetical quantum
generalization)
Now the transformations T11 and T12
will be:
T11: 1/nf à n }
T12:
n à n2+f
}
The true generalized result of the relative
fractal dimension is
log(n2+f)/log(n) = 2+f, with the
expression (1): (δ+ε)/δ = 2+f (4)
During the transition of dimensions, the value
of the fictitious coefficient f, associated with the very nature of the
quantum (hypothetically), was defined. We will analyze the transition of
dimensions combining expressions (3) and (4), for ε=9−δ:
(En)(n(ε−δ)/δ) <Constant.
Multiplying and dividing by nδ which is
the generalized volume to ordinary dimensions δ:
(Energy_density)
(nφ)<Constant. The value of φ = (δ2−2δ+9)/δ and
is represented in figure 2.
For δ = 3 there
is a minimum that corresponds to a maximum in energy density. For δ = 0, the
value is infinite and corresponds to a minimum density equal to zero. The transition of dimensions from δ = 0,
ordinary dimensions, to δ =
3, ordinary dimensions, takes us from a vacuum energy equal to zero to a
maximum value. “In particular, our laws of physics arise from the geometry
of the extra dimensions. Understanding this geometry ties string theory to
some of the most interesting questions in modern mathematics, and has shed new
light on them, such as mirror symmetry” (Polchinski,
2015)
5
Conclusion
It is possible that there was a transition of
dimensions that maximized the energy density of the vacuum for δ=3 (ordinary
dimensions) and ε=6 (compact dimensions). The nature of the quantum of action
may be tied to these specific values of δ and ε.
References
Mandelbrot, B.
(1987), Los objetos fractales,
Barcelona, Tusquets Editores.
Polchinski, J. (2015), String theory to the rescue. ArXiv: 1512.02477 v5 [hep-th]
Ruiz-Fargueta,
J.S. (2004) El sorprendente vacío
cuántico. Revista Elementos Universidad de Puebla BUAP.MX, 53, pp.52-53. (16/01/2022)https://elementos.buap.mx/directus/storage/uploads/00000002608.pdf